GJK(Gilbert-Johnson-Keerthi)算法
背景知识
凸多边形
- 定义:对于平面上的一个多边形,如果延长它的任意一条边,使整个多边形都位于延长线的同侧,这样的多边形为凸多边形
显然,人可以直观的判断一个多边形是否为凸多边形,那么在程序中,应该如何判断一个多边形是否为凸多边形
利用向量的叉乘,根据多边形顶点坐标,依次求出每条边的向量axb,bxc,cxd…的结果应同号,否则就为凹多边形
闵可夫斯基和
闵可夫斯基和是两个欧几里得空间点集的和。点集A与B的闵可夫斯基和用公式表示就是 A+B={a+b∣a∈A,b∈B}
对于减法,闵可夫斯基和的概念也成立,即为闵可夫斯基差,举个例子
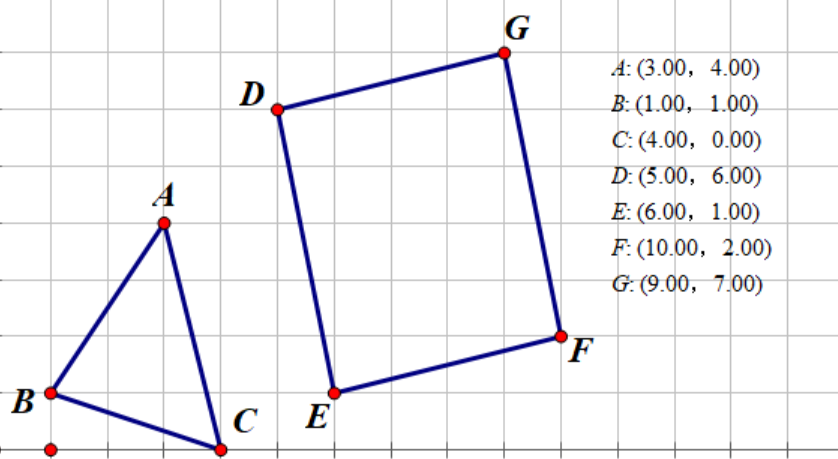
下面这两个图形的闵可夫斯基差即为
A−B={(3−5,4−6),(3−6,4−1),(3−10,4−2),(3−9,4−7)(1−5,1−6),(1−6,1−1),(1−10,1−2),(1−9,1−7)(4−5,0−6),(4−6,0−1),(4−10,0−2),(4−9,0−7)}
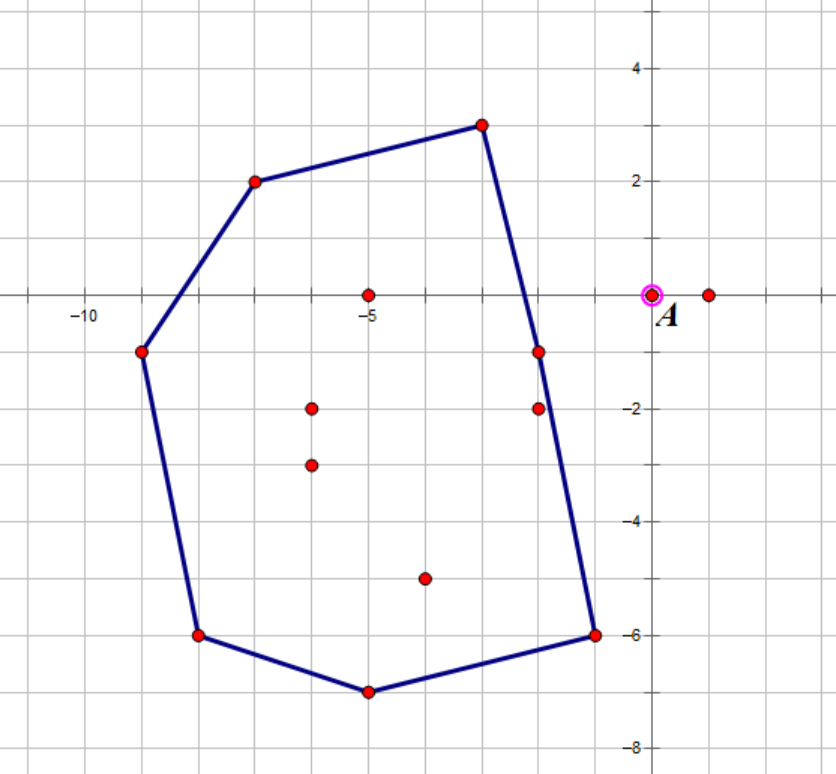
这是两个不相交的图形的闵可夫斯基差,下面看看若两个图形相交的闵可夫斯基差

可以看到,对于两个相交的图形,他们的闵可夫斯基差是包括原点的,且两个多边形之间的距离就是其闵可夫斯基差到原点的距离。下面解释一下为什么相交的多边形一定包含原点,很好理解,若两个多边形相交,那么他们之间一定存在一个公共点,相减即为(0,0)。
单纯形
k阶单纯形,一个k维单纯形是指包含(k+1)个节点的凸多面体。
例如0阶单纯形就是点,1阶单纯形就是线段,2阶单纯形就是三角形,3阶单纯形就是四面体。对于2维空间的多边形,最多用到2阶单纯形。
对于上面两个相交的多边形的例子,实际运用中,不需要求出完整的闵可夫斯基差,只需要在闵可夫斯基差内形成一个多边形,使其尽可能包含原点即可,这个多边形就是单纯形。即若单纯形包好原点,纳闷闵可夫斯基差也一定包含原点。
Support函数
Support函数的作用是计算多边形在给定方向上的最远点。在构建单纯形时,我们希望尽可能得到闵可夫斯基差的顶点,这样产生的单纯形才能包含最大的区域,增加算法的快速收敛性。
向量的点乘与叉乘
点乘用于判断两个向量是否同向,叉乘用来判断点在线段的左侧还是右侧。
GJK算法
核心逻辑
给定两个多边形p和q,以及一个初始方向,通过迭代的方式构建,更新单纯形,并判断单纯形是否包含原点,若包含原点则两个多边形相交,否则不相交。
算法步骤
- 选取初始方向,初始方向可以是两个多边形的中心点构成的矢量,也可以是两个多边形各自选取的一个顶点构成的矢量,还可以是给定的任意矢量
- 根据初始方向,用Support函数得到第一个Support点,并放到单纯形(simplex)中
- 将初始方向取反,作为下一次迭代方向
- 循环开始:
- 根据迭代方向和Support函数,计算出一个新的Support点
- 若新的Support点与迭代方向的点乘小于0,说明在这个迭代方向上,已经无法找到一个能够跨越原点的Support点了,也就是说,无法组成一个能包含原点的单纯形。即两个多边形不相交,函数退出
- 若新的Support点能够跨越原点,则将其加到simplex中
- NearestSimplex函数用来更新单纯形和迭代方向,并判断simplex是否包含原点。这是simplex有两个点或三个点:
- 若为两个点,则这两个点构成一条直线,以该直线的垂线朝向原点的方向,作为下一次迭代方向
- 若为三个点,则需要判断这三个点组成的三角形是否包含原点。若不包含,则保留离原点最近的边上的两个点,同样以这两个点的直线的垂线朝向原点的方向作为下一次迭代方向
- 回到循环开始步骤
关于跨越原点,可以理解为过原点做一条垂直于方向的直线,若两个点在直线两侧,则为跨越原点
实现细节
用一个类来表示向量,支持向量的点乘,加减,与法向量的计算
Support函数
利用向量的点乘找出方向向量上的最远点
判断三角形是否包含原点
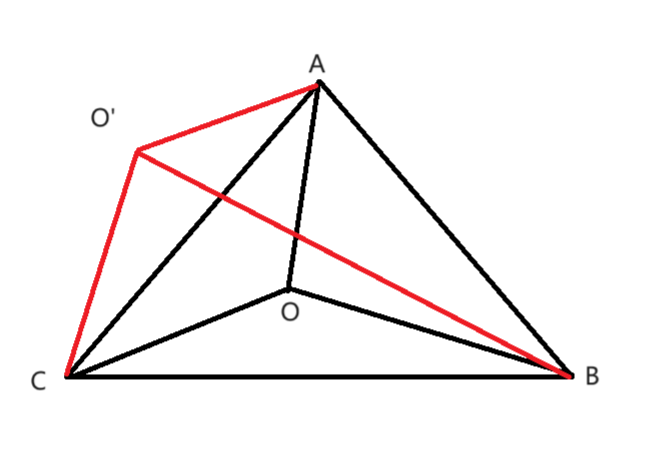
对于一个三角形,若O点在三角形内部,显然 S△ABC=S△AOC+S△AOB+S△BOC,若O在三角形外部,那么 S△ABC<S△AOC+S△AOB+S△BOC,所以只需要能够计算出这些面积就能判断O点是否在三角形内部了,直接用海伦公式就行了
找出离原点最近的边上的两个点
要求这个相当于求原点到边的距离,及某一点到某一边的距离,用代码实现点到直线的距离即可
参考代码
#include <iostream>
#include <vector>
#include <limits>
#include <cmath>
class Vector2D {
public:
double x, y;
Vector2D(double _x = 0, double _y = 0) : x(_x), y(_y) {}
Vector2D operator - (const Vector2D& other) const
{
return Vector2D(x - other.x, y - other.y);
}
double dot(const Vector2D& other) const
{
return x * other.x + y * other.y;
}//向量的点乘
Vector2D perp() const
{
return Vector2D(-y, x);
}//计算法向量
Vector2D operator-() const
{
return Vector2D(-x, -y);
}
}origin(0,0);
Vector2D support(const std::vector<Vector2D>& shape1, const std::vector<Vector2D>& shape2, const Vector2D& dir) {
double maxDot = -std::numeric_limits<double>::infinity();//返回正无穷大
Vector2D bestPoint;
for (const auto& p : shape1) {
double dotProduct = p.dot(dir);
if (dotProduct > maxDot) {
maxDot = dotProduct;
bestPoint = p;
}
}//找出最远点
Vector2D pointOnShape2;
maxDot = std::numeric_limits<double>::infinity();
for (const auto& p : shape2) {
double dotProduct = p.dot(dir);
if (dotProduct < maxDot) {
maxDot = dotProduct;
pointOnShape2 = p;
}
}//找出最远点
return bestPoint - pointOnShape2;//作差
}
double calcPointToPointDistance(Vector2D p1, Vector2D p2)
{
return sqrt(pow(p1.x - p2.x,2) + pow(p1.y - p2.y,2));
}
double calcPointToLineDistance(Vector2D p0, Vector2D p1, Vector2D p2)
{
double k = (p2.y - p1.y) / (p2.x - p1.x);
double A = k, B = -1, C = p1.y - k * p1.x;
return fabs(A * p0.x + B * p0.y + C) / sqrt(A * A + B * B);
}//计算p0到p1与p2构成的边之间的距离
double calcTriangleArea(Vector2D p1, Vector2D p2, Vector2D p3)
{
double a = calcPointToPointDistance(p1, p2);
double b = calcPointToPointDistance(p1, p3);
double c = calcPointToPointDistance(p2, p3);
double p = (a + b + c) / 2.0;
return sqrt(p * (p - a) * (p - b) * (p - c));
}//海伦公式计算面积
bool isContainOrigin(Vector2D p1, Vector2D p2, Vector2D p3)
{
double s1 = calcTriangleArea(origin, p1, p2);
double s2 = calcTriangleArea(origin, p1, p3);
double s3 = calcTriangleArea(origin, p2, p3);
double s = calcTriangleArea(p1, p2, p3);
if (fabs(s1 + s2 + s3 - s) < 1e-6)
return true;
return false;
}
bool GJK(const std::vector<Vector2D>& shape1, const std::vector<Vector2D>& shape2){
// 初始化单纯形
std::vector<Vector2D> simplex;
Vector2D direction = {1, 0}; // 初始方向
simplex.push_back(support(shape1, shape2, direction));
direction = -simplex[0];//方向取反
while (true) {//开始循环
simplex.push_back(support(shape1, shape2, direction));
if (simplex.back().dot(direction) <= 0)
return false; //点乘小于0,不可能相交
if (simplex.size() == 3)
{
if (isContainOrigin(simplex[0], simplex[1], simplex[2])){
return true;
}// 判断当前单纯形的三个顶点组成的三角形是否包含原点
double minDistance;
int minIndex1 = -1, minIndex2 = -1;
for (int i = 0; i < 3; i++){
for (int j = i + 1; j < 3; j++){
double distance = calcPointToLineDistance(origin, simplex[i], simplex[j]);
if (minIndex1 == -1 || distance < minDistance){
minDistance = distance, minIndex1 = i, minIndex2 = j;
}
}
}// 找到三角形离原点最近的边
Vector2D line = simplex[minIndex1] - simplex[minIndex2];
direction = line.perp();
int k = 3 - minIndex1 - minIndex2;
simplex.erase(simplex.begin() + k);//删除剩下的那个点
}
else
{
Vector2D line = simplex[0] - simplex[1];
direction = line.perp();
}
}
}
int main() {
std::vector<Vector2D> shape1 = {{3, 4}, {1, 1}, {5, 1}};
std::vector<Vector2D> shape2 = {{4, 3}, {4, 0}, {7, 3},{7,0}}; //初始化两个图形的顶点坐标
if (GJK(shape1, shape2))
std::cout << "Shapes intersect.\n";
else
std::cout << "Shapes do not intersect.\n";
return 0;
}
|
参考资料碰撞检测算法之GJK算法




